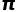 是数学中至关重要的一个数,相信大家都知道圆周率的含义(圆的周长与直径的比值),但是大家知道圆周率的值是如何求出的吗?你知道利用家中常见的针或者小米,也能计算圆周率吗?
是数学中至关重要的一个数,相信大家都知道圆周率的含义(圆的周长与直径的比值),但是大家知道圆周率的值是如何求出的吗?你知道利用家中常见的针或者小米,也能计算圆周率吗?古人在很久以前便意识到了圆的周长与直径的比值是一个定值,并且对这个值进行了粗略的测量,测量方法是直接对圆的周长与直径分别测量之后作比。
但因古代所绘圆形并不是完美的圆,且测量精度不够,所以用这种方法得出的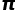 值有较大的误差,唐朝杨炯所的《浑天赋》一文中写到:“周三径一,远近乖於辰极;东井南箕,曲直殊於河汉。”可见,古代人们认为
值有较大的误差,唐朝杨炯所的《浑天赋》一文中写到:“周三径一,远近乖於辰极;东井南箕,曲直殊於河汉。”可见,古代人们认为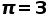 。
。
其实,早在三国时期,中国的数学家刘徽便发明了一种精确计算圆周率的方法:割圆术。这也是中国数学史上第一个从数学上计算圆周率到任意精确度的迭代算法。
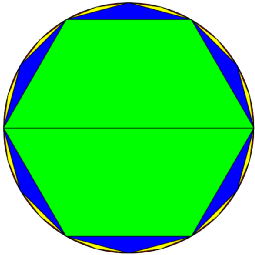
割圆术原理:绿色为六边形,蓝色为十二边形,可以看到十二边形面积与圆面积更接近,若边数继续增加,其面积与圆形就更接近 图片来源:wikipedia
 的基础之上的。
的基础之上的。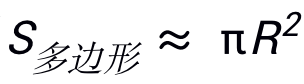 从而得出
从而得出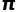 的值。
的值。 ,是此后近千年世界上最准确的圆周率数值。
,是此后近千年世界上最准确的圆周率数值。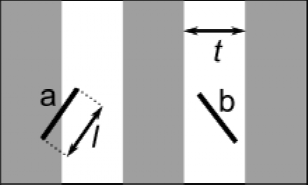
布丰投针问题 图片来源:wikipedia
布丰投针答案的得出需要一定的概率论和微积分知识,本文不详细叙述推导过程。如果针长度为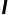 ,平行线之间的长度为
,平行线之间的长度为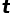 且
且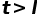 ,我们可以得到针和纹路相交的概率为:
,我们可以得到针和纹路相交的概率为: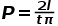 。
。
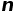 次针,其中有
次针,其中有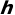 只与纹路相交,那么此时
只与纹路相交,那么此时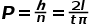 。这时候,我们便可以知道
。这时候,我们便可以知道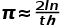 ,实际抛针数越多,计算出来的
,实际抛针数越多,计算出来的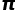 就越精确。
就越精确。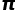 值需要投掷很多次针,可能会有一定的危险。所以,接下来我给大家介绍一种利用一张纸和小米便能够完成的0危险的计算
值需要投掷很多次针,可能会有一定的危险。所以,接下来我给大家介绍一种利用一张纸和小米便能够完成的0危险的计算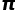 的方法——利用圆面积公式的蒙特卡洛方法。
的方法——利用圆面积公式的蒙特卡洛方法。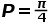 。如果我们投掷了
。如果我们投掷了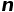 个点,其中有
个点,其中有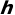 个在四分之一圆中,那么我们便可以知道
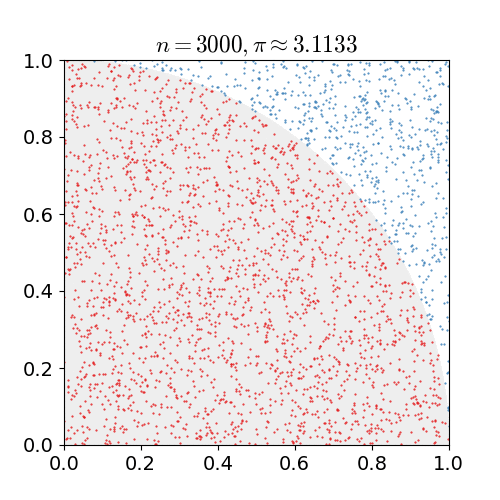
个在四分之一圆中,那么我们便可以知道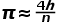 。
。
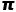 值 图片来源:wikipedia-nicoguaro
值 图片来源:wikipedia-nicoguaro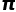 的足够精准的值,我们投掷的次数n需要很大,所以这种实验一般在计算机上进行,如果我们利用小米与纸张来进行这个实验的话,可能会需要花费很长时间来对小米进行计数了(当然对我们的眼力也是一个挑战)。
的足够精准的值,我们投掷的次数n需要很大,所以这种实验一般在计算机上进行,如果我们利用小米与纸张来进行这个实验的话,可能会需要花费很长时间来对小米进行计数了(当然对我们的眼力也是一个挑战)。3
圆周率,无处不在
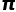 在数学中有着极为重要的意义,而不是仅仅用来计算圆的面积。有很多时候,
在数学中有着极为重要的意义,而不是仅仅用来计算圆的面积。有很多时候,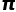 会在你意想不到的问题中突然出现。比如数学中一个知名问题:巴塞尔问题。
会在你意想不到的问题中突然出现。比如数学中一个知名问题:巴塞尔问题。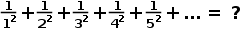 。
。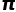 有什么关系。但是,欧拉在1735年给出的证明指出,该级数的和为
有什么关系。但是,欧拉在1735年给出的证明指出,该级数的和为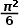 。这让数学界大跌眼镜,欧拉也因此声名大噪。
。这让数学界大跌眼镜,欧拉也因此声名大噪。4
现代的圆周率求法
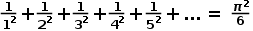 那我们可不可以利用这个式子来计算
那我们可不可以利用这个式子来计算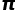 呢?
呢?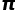 的计算都是应用级数法来解决的。
的计算都是应用级数法来解决的。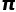 的效果并不好,算到几百项
的效果并不好,算到几百项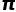 的精度还没有祖冲之来得高。这时,一个神人的出现改变了这个现象,他就是数学鬼才:斯里尼瓦瑟·拉马努金。
的精度还没有祖冲之来得高。这时,一个神人的出现改变了这个现象,他就是数学鬼才:斯里尼瓦瑟·拉马努金。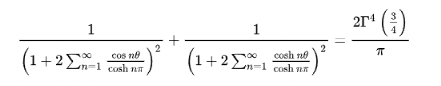
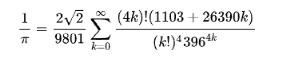
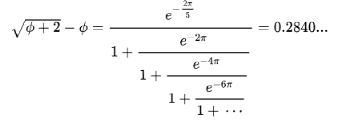
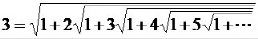
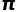 的十几项。现在数学家已经利用这个公式算出了
的十几项。现在数学家已经利用这个公式算出了 后的62.8万亿位。
后的62.8万亿位。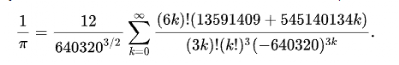
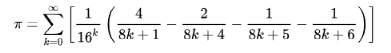
 会有一些特殊的性质,比如被算尽、在某一位后循环,或者被表示成为一些更为简单的代数式。
会有一些特殊的性质,比如被算尽、在某一位后循环,或者被表示成为一些更为简单的代数式。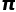 是一个超越数,也就是说
是一个超越数,也就是说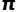 不是任何代数方程的根,其不能被表达为长度有限的代数数组成的代数式的形式,我们只能用上文中那种无穷级数或者积分来精准表示
不是任何代数方程的根,其不能被表达为长度有限的代数数组成的代数式的形式,我们只能用上文中那种无穷级数或者积分来精准表示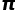 的值。
的值。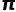 有了新的猜想,他们认为
有了新的猜想,他们认为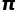 是一个“正规数”,也就是说每一个数在中出现的概率是均等的,这个猜想没有被证明。
是一个“正规数”,也就是说每一个数在中出现的概率是均等的,这个猜想没有被证明。 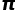 中含有所有的8位数,这意味着我们的生日、我们的毕业典礼、我们的结婚纪念日……一切的日期都会在
中含有所有的8位数,这意味着我们的生日、我们的毕业典礼、我们的结婚纪念日……一切的日期都会在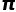 中出现,不如现在就去查查自己的生日在
中出现,不如现在就去查查自己的生日在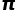 中第几位?
中第几位?6
我们有必要了解圆周率吗?
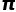 ,
,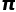 中仍然隐藏着无穷的秘密,等待着人类前去探索。
中仍然隐藏着无穷的秘密,等待着人类前去探索。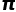 了”。
了”。来源:科普中国




请输入验证码